Finance Basics:
Annuities
This short article will give you a general understanding of annuities. Annuities are a special type of cash flow where each year you get a specified amount of money. There two basic types of annuities.
- Normal annuity: This type of cash flow is received at the end of each period (typically a year)
- Annuity due: When you get a cash flow periodically at the beginning of each period.
We can further divide annuities. The following two types of annuities can also be either normal, or annuity due.
- Perpetuity: You receive the annuity forever. A very typical example is life annuity (or life rent).
- Growing perpetuity: This is a special annuity where there is also a growth factor, but the factor is constant. In other words, each period the growth is the same rate. Please note that it is the same growth rate, not the same amount!
These terms, and their application is essential in understanding bonds, shares, etc because they are the basis of how we can determine their market price and value (among other things).
Normal annuity -- Present and future value
If you have read the article on Present and future value, you know by now how to calculate them. Normal annuity is no different, because all we have to do is calculate PV of FV for each of the periods. Of course that would be quite long for an annuity which has a lifespan of 50 years. Luckily we have a shortcut. Lets look at a short example and calculate future value with the long and the short way.
Example:
Part of your portfolio is bonds. One particular bond will pay you $1000 for five years at the end of each year. What is the present value of the cash flows if the interest rate is 10%?
The solution can be shown on a timeline:
I have looked up PVIF for each year, for each amount. If you look at the tables in the Value of money article you will find PVIF10,1 to be 0,909 ; PVIF10,2 to be 0,826 and so on.
If we would calculate Present value each time, we would get 909, 826 and so on (
). If we add these values up, we would get 3791. Alternatively we can add up all the PVIF values and then multiply by 1000. This is the basis for the short cut. We also have tables for PVIF values added up. These are called Present Value Interest Factors Annuity, or PVIFA. If you look up PVIFA10,5 you would get 3,791, which would be the same as PVIFA10,1 + PVIFA10,2 + PVIFA10,3 + PVIFA10,4 + PVIFA10,5.
Future value for annuities needs no more explanation because it works in exactly the same way. You add up all the FVIF values and multiply by the amount of the cash flow (remember to only multiply by the amount/period, not the total amount). The sum of these would give you the FVIFA amount.
Annuity Due -- Present and Future value
Annuity due is different from normal annuity because you get each cash flow amount in the beginning of the period. The calculation matches the one before, but a methodical difference is very important to remember. Present value for annuity due is larger, while future value is a smaller amount than for normal annuity. To understand this we (again) look at some timelines and seek the help of present value.
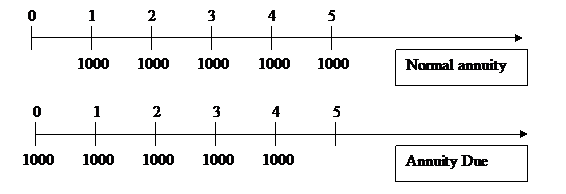
You can see that with normal annuity the first value is PVIF10,1 while the first value for annuity due is PVIF10,0 which would be 1, in other words the original cash flow amount (because we want the value of the money in the present, but we are in that present). So when calculating present value for normal annuities we multiply each amount by a value that is less than one. For Annuity due we multiply every value with a number less than one, except the first which is multiplied by on itself, so the whole sum is bigger. This may not seem like a big difference, because instead of 3,791 we multiply with 4,169 ; this almost 0,4 difference can be huge if your cash-flow is $1000000!
The future value for annuity due is smaller for the same reason. For future value FVIF will always be a number larger than one, except for the first year where it will be one, so the total sum will be a smaller number.
Please do not be mislead by the number of years on the timelines. While you get your last $1000 at year four, that is the beginning of period five.
Of course there is a short cut for calculating annuity due also. We do not make tables for this (although it can be done for speed's sake), we can calculate it using the following:
If you want to know what the result of our example would be if we would use annuity due, than look up PVIFA10,4 and add 1. These equations are a direct result of what we have discussed. You use all the PVIF values for annuity due as for normal annuity, except for the last one, because you got your cash-flow in the beginning of the period, so your first one was at year 0. This amount is 1, so that is why you add one at the end.
The logic behind future value is much the same, I feel there is no need for further explanation.
Perpetuity
Perpetuity is a term for unlimited amounts of cash-flow. Because of the nature of this we cannot use the previous ways to calculate the value of the annuity. We use a very simple equation, but I will not explain it because the mathematics behind it is quite complicated.
Example:
By winning the Nobel prize let's say that you are entitled to $20000 every year for the rest of your life. What is the total worth of your prize if the interest rate is 15%?
We can say that the prize is worth $133333,34 today.
Growing perpetuity
This is a perpetuity which increases each year by a fixed rate. Again we will not discuss the equation because the mathematical derivation is long and unimportant for our purpose.
Example:
If by winning the nobel prize you get $20000 each year plus a 5% increase you can calculate the present value using the above equation:
Please familiarize yourself with this article especially before moving on to the article on bonds because it relies heavily on the material discussed here.
Information is for educational and informational purposes only and is not be interpreted as financial or legal advice. This does not represent a recommendation to buy, sell, or hold any security. Please consult your financial advisor.